| OCR Text |
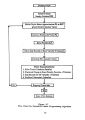
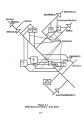
Show Table 5.1 Constraint/ Objective Function and Decision Variable Dependence for Single Reservoir Model Decision Function Variable IS£ EA2. US£ Q££ Q& l Mr im x x xx Irli x x x xx Hi x x x xx Dj x x x xx Fj x x x xx considered. It is assumed that a prior identification of the pattern ( lag and lag coefficients) of return flows from the demand areas is also possible. The possibility of either diverting M& I and Irrigation releases through the hydropower plant, or bypassing the hydropower plant is also considered. Flood control and conservation storages are considered admissible at each site, as well as recreation benefits. Reservoirs are numbered sequentially from upstream to downstream. This allows the algorithm developed to proceed sequentially from upstream to downstream sites, evaluating the total release from an upstream reservoir, and using it to determine the total inflow ( local plus upstream releases plus return flows) at the downstream reservoir. The model formulated thus leads to a sequential reservoir screening algorithm, with criteria for the conjunctive operation of reservoirs satisfied by a simultaneous examination of the reduced gradients with respect to all decision variables and constraints. With the general scenario as described above, the extension of the formulation to the multi- reservoir case is readily attained. As before, the decision variables are the yields Mr sm, Ir sj, Hs, the storages Ds, and Fs for each reservoir s and each demand area ( m or i). In addition a decision variable Xsz that denotes the fraction of the total monthly outflow ( Hydro release + spills) that is diverted off- stream to a reservoir z is also considered. Decisions on the annual M& I and irrigation releases ( for each specified reliability) from each reservoir to each demand area, the firm annual hydropower release from each reservoir, the fraction of the release from a reservoir diverted to another reservoir, the dead storage at each reservoir and the flood storage provided at each reservoir, are thus explicitly considered. The constraints and the objective function for the optimization model are similar to those specified for the single reservoir formulation. The evaluation of the functional relationships between storage capacity, costs, hydropower net revenue and the decision variables, however is slightly more complex, since the simulation process needs to account for the physical networking of the reservoir system and the associated monthly mass balance considerations. The modifications needed for the evaluation of the nonlinear functions through simulation are described first followed by a statement of the model. 115 |