| OCR Text |
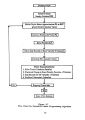
Show functionally relates the yields to the storage requirements and economics through an internal simulation of the attendant hydrology was formulated. At the root of the formulation is the observation that there is a direct functional relationship at each site between the yield specified and the storage required at the site. An optimization model that directly develops and exploits this relationship with the associated economics is likely to be more computationally efficient and compact than one that directly solves for month by month releases from the reservoir, as well as for the reservoir size. There is likely to be some accompanying loss in the efficiency/ flexibility of reservoir operation, since the operation rules would of necessity have to be pre- specified. However, in light of Klemes's ( 1979) argument and the reconnaissance nature of the exercise, it may not be significant. 5.2 Literature Review : Loucks et al ( 1981) provide a review of selected reservoir design and screening models. Stedinger et al ( 1983) review and compare several screening models. Models of reservoir system operation are more common in literature than are models for preliminary reservoir selection and screening. Reservoir operation models are often imbedded in the scheme for reservoir sizing. The approach contemplated in this study does not require the incorporation of a full scale reservoir operation optimization procedure in the reservoir sizing problem. Consequently, the entire reservoir operation literature is not reviewed. The reader is referred to Yeh ( 1985), Loucks et al ( 1981), and Rosenthal ( 1980) for general reviews of the reservoir operation and management literature. Deterministic models presume that hydrologic and other parameters are known'. Historical data ( e. g. monthly or average monthly flow values) is accepted as a descriptor of likely future occurrences, and system designs are based on reservoir operation with this data set. Explicitly stochastic models view the historical data set merely as a single representation of reality, the design situation as one characterized by uncertainty, and explicitly consider hydrologic uncertainties and system reliability. Implicitly stochastic models explicitly consider the reliability of reservoir yields and implicitly incorporate a measure of the probability distribution of natural unregulated flows through the consideration of historical data ( such as critical period flows). All three kinds of models were reviewed to synthesize a viable formulation for our project's needs. Stedinger et al ( 1983) provide a comparison of the modeling considerations and results using all three types of formulations referred to above. Stedinger et al's ( 1983) conclusions were that ( 1) simple screening models that can identify potentially efficient system designs are highly desirable; ( 2) purely deterministic screening models based on historical mean monthly flows do not provide sufficient reservoir capacity to achieve target reliabilities, ( 3) use of the most critical flows in a record leads to larger reservoir capacities and higher system reliabilities; ( 4) the explicitly stochastic models - linear decision rule, chance constrained formulations of Revelle et al ( 1969) and Loucks ( 1970) overestimated reservoir capacity and generated operating policies that failed to utilize available water and storage space efficiently; and ( 5) the yield model of Loucks et al ( 1981) produced reasonable reservoir system designs with release reliabilities near the targets. The ' yield model' presented by Loucks et al ( 1981) and compared to other techniques by Stedinger et al ( 1983) provides the motivation for the model eventually developed here. They presented a general formulation considering only water supply operation for single and multi- reservoir sizing. A hypothetical case- study ignoring evaporation, seepage and precipitation is presented by Stedinger et al ( 1983) for a three reservoir ( in parallel) configuration. The approach stresses that given a streamflow sequence, reservoir storage capacities required to deliver various yields with given 104 |