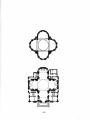
| Show EPISTEMOLOGY Theory of knowledge. All disciplines have their theories of knowledge pertaining to that subject matter. Architecture is about environmental space and since geometry is not about space there is no knowledge to be had on the subject of environment in the first place. You can not know a point or a line or a plane since they don't exist. Architecture is a psuedo discipline. EUCLID The Greek mathematician who gave us plane geometry and the definitions of point line and plane. EUCLIDIAN SPACE Environment that is modeled on Euclid's definitions. NOTE: Many of these definitons lead to circular thinking and hence the nonsense inherent in architecture as a so called discipline. FLOOR PLAN METAPHYSICS The psychology of nothingness as the architect organizes a house or any building in adherance to the client's specifications. See diagram in the text. Walls are planes which have no epistemological reality except in the mind of the architect. GESTALT KNIT The merger of two whole continumorphic spaces into one larger whole. The result of part whole reciprocation. The general combining of parts into wholes. GIVEN DATA BASE A series of sets that are prescribed to provide the components of any number of unprescribed spaces or floor plans. Unlike a required data base no plans have yet been created. HYPOCRITICAL DUALISM The contridiction between man and nature. The contridiction between man made environment and the landscaping that is put to coverup to give the blank planes the variety we long for. IMPLIED CONTINUMORPHS The naturalistic hypocrisy effects the urge for continumorphs an implied series of continumrophs. In place of continumorphs we have a nuerotic dualism a hypocrisy between man and nature. Modern buildings often reflect an urge for differentiation in the otherwise blank planes called walls. INFINITE SETS Continumorphs occure in morphic themes - polyhedrons which share common topology but differ in size and aspect - no two in a set are exactly alike hence there are endless numbers of continumorphs in each series or set. -98- |