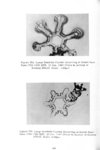
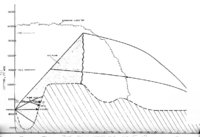
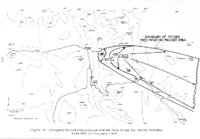
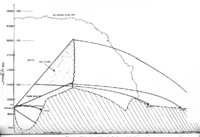
Contents | 47 of 392
Page 47
| Title | Park range atmospheric water resources program |
| Creator | Rhea, J. Owen ; Willis, P.; Davis, L. G. |
| Subject | Weather control; Park Range (Colo. and Wyo.) |
| Publisher | Bureau of Reclamation |
| Contributors | Bureau of Reclamation |
| Date | 1969 |
| Type | Text |
| Format | application/pdf |
| Identifier | Orhea_Park_Range_Atmospheric.pdf |
| Language | eng |
| Rights Management | http://rightsstatements.org/vocab/NoC-US/1.0/ |
| Call Number | QC928.O7 |
| ARK | ark:/87278/s64f7fp7 |
| Setname | wwdl_books |
| ID | 1609981 |
| Reference URL | https://collections.lib.utah.edu/ark:/87278/s64f7fp7 |
Page Metadata
| Title | Page 47 |
| Format | application/pdf |
| Setname | wwdl_books |
| ID | 1610028 |
| Reference URL | https://collections.lib.utah.edu/ark:/87278/s64f7fp7/1610028 |