| Title |
LIM Simulations of Mixing and Chemical Reaction in Gas Reburning Applications |
| Creator |
Suresh, Nallan C.; Dahm, Werner J.A.; Tryggvason, Gretar |
| Publisher |
University of Utah |
| Date |
1996 |
| Spatial Coverage |
presented at Baltimore, Maryland |
| Abstract |
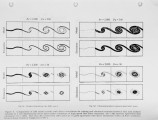
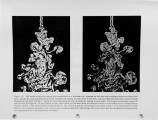
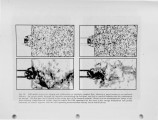
Achieving high NOx removal efficiency with gas reburning in any given installation requires tailoring the gas injection and mixing scheme to the distributions of temperature and NOx within the furnace. The injection scheme must also be robust enough to accommodate changes in these distributions under varying furnace load conditions. These considerations suggest that advanced modeling of the reburn gas injeclion and mixing can greatly assist effective implementation of reburn technology in most installations. Results are presented from local integral moment (LIM) simulations of gas injection and mixing for reburning applications. The LIM approach is fundamentally different from classical turbulence models. It uses the fact that molecular mixing processes in turbulent flows are concentrated on universal, self-similar, small-scale structures. The model incorporates this through a local parabolization of the complete time-dependent governing transport equations on the time-evolving material surface on which gradients are concentrated. This leads to a closed set of equation governing the local integral moments along the layer-normal direction at each point on the surface, effectively transforming the original partial differential equations to a set of ordinary differential equations that can be solved on a time-evolving surface. Results from validalion cases indicate that LIM simulations can provide accurate insights into the complex now and mixing processes that are essential to successfully implementing gas reburn in any given installation. |
| Type |
Text |
| Format |
application/pdf |
| Language |
eng |
| Rights |
This material may be protected by copyright. Permission required for use in any form. For further information please contact the American Flame Research Committee. |
| Conversion Specifications |
Original scanned with Canon EOS-1Ds Mark II, 16.7 megapixel digital camera and saved as 400 ppi uncompressed TIFF, 16 bit depth. |
| Scanning Technician |
Cliodhna Davis |
| ARK |
ark:/87278/s63t9ktx |
| Setname |
uu_afrc |
| ID |
10355 |
| Reference URL |
https://collections.lib.utah.edu/ark:/87278/s63t9ktx |