| OCR Text |
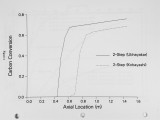
Show D I S C H A I N was developed as a compromise between simplistic rate correlations and detailed mechanistic models. The integro-differential equation for bridge dissociation (like that for the D A E M ) is difficult to integrate over arbitrary particle temperature histories, and the additional five differential equations make D I S C H A I N more computationally expensive then the simpler models. The intent of this paper is to show the sensitivity of coal combustion calculations to these different devolatilization models. Kinetic parameters for these models, obtained by comparison with experimental data and reported in the literature, are shown in Table 3. Calculations are performed to simulate (1) a well-controlled, laminar flow, single particle experiment (Mitchell et al., 1985), and (2) pulverized coal combustors. The laminar flow simulations provide a well-controlled numerical experiment that facilitates interpretation of results, while the combustor simulations show implications of the information learned from the laminar flow simulations. LAMINAR FLOW REACTOR SIMULATION Mitchell et al. (1985) have measured particle size, temperature, and velocity in a laminar flow reactor in order to obtain global char oxidation rates; a laminar CH4-air flame provides the gas environment into which single particles are injected. Mitchell performed detailed measurements of the gas conditions (i.e. temperature, velocity, and composition) for his char oxidation studies, and notes the location of the luminous zone which indicates the devolatilization region. In our study we simulate a coal particle flowing through this reactor using the various models of devolatilization previously described. The gas velocity (vg) for this simulation is related to the gas temperature (Tg) by the following equation (taken from Mitchell et al., 1985): 1 / C2W ,„\ where w = zTg Jb7bb. (9) Equation 8 represents the solution of the momentum equation in a square conduit with consideration of the boundary layers developing separately on each wall. Gas temperatures are measured at 9 different heights (z) above the burner for each gas condition, and the constants cj and c2 are determined by least squares fit of the velocity measurements. Particle velocity and temperature are calculated from the equations of conservation of particle m o m e n t u m and energy: dvp -18iig(vp - vg)(l + 0.15#e0-687) - 9, (10) 4 |