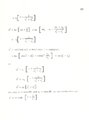| Description |
The study of minimal surfaces is an active branch of mathematics, with many questions yet to be answered. One major question that was answered in 1985 was whether the plane, the catenoid, and the helicoid are the only complete embedded minimal surfaces in R3 of a finite topological type. In [4] Hoffman and Meeks proved that the answer to this question is that other surfaces of this type do exist, and they proved this by finding an example. We discuss that example here, but rather than prove that the surface is complete and embedded we concern ourselves mainly with the shape of the surface. |